viernes, 24 de febrero de 2012
jueves, 23 de febrero de 2012
Modulación por posición de impulsos
en este caso, la señal moduladora produce un desplazamiento de los pulsos a la posición de estos en ausencia de modulación.
una de las principales dificultades en la implementación de esta técnica es que el receptor debe estar debidamente sincronizado para poder alinear el reloj local con el inicio de cada símbolo.
por este motivo se implementa usualmente de manera diferencial como modulación por posición de impulso diferencial donde la posición de cada pulso es elegida en función del pulso anterior y de esta manera el receptor solo debe medir la diferencia de tiempo entre la llegada de los sucesivos pulsos.con este tipo de modulación un error en el reloj se podría propagar solo a la medición de dos pulsos adyacentes en vez de toda la transmisión.
Consiste en desplazar los pulsos desde una posición de referencia hasta otra, en función del valor de la señal f(t). El mínimo desplazamiento de pulso se usa para designar el mínimo valor de f(t) y el cambio de posición es proporcional a la señal moduladora f(t).
Una forma conveniente de generar PPM es usar la señal PWM generada y entonces accionar un generador de pulsos de ancho constante en los flancos de bajada de la señal PWM.
el circuito generador de pulsos puede ser considerado como un monoestable el cual se dispara con el flanco de caída de la señal de
PWM el ancho del pulso generado se termina por el monoestable.
Sensibilidad a la interferencia por caminos Múltiples
Dejando de lado las cuestiones relativas a la sincronización del receptor la principal desventaja de la MPP es que es de por si muy sensible a la interferencia por caminos múltiples que surge en canales con desvanecimientos selectivos en frecuencia donde la señal en el receptor contiene ecos de los pulsos transmitidos. Dado que la información está codificada en el tiempo de llegada ya sea de manera diferencial o relativa a un reloj común la presencia de estos ecos hace que sea extremadamente difícil si no imposible poder determinar con precisión la posición correcta del pulso transmitido.
lunes, 20 de febrero de 2012
HISTORIA DEL TELÉGRAFO
La palabra telégrafo proviene de las palabras griegas tele que significa lejos y grapho escribir. su significado es "escribir a distancia".
la telegrafía tiene orígenes muy antiguos.sus antecedentes más remotos se encuentran en los redobles de tambores y en las señales de humo
El primer telégrafo fue inventado por Claude Chappe en 1794. era un sistema visual
utilizaba una bandera basada en el alfabeto y dependía de una linea de visión para la comunicación
posteriormente este telégrafo fue sustituido por el telégrafo eléctrico.en 1809 un telégrafo fue inventado en Baviera por Samuel Soemmering. utilizo 35 cables con electrodos de oro en agua. la comunicación terminaba a una distancia de 2,000 pies y era detectada por la cantidad de gas generado por los electrodos.
en 1828 Harrison Dyar invento el primer telégrafo de los EEUU que enviaba chispas eléctricas a través de una cinta de papel tratado químicamente para grabar puntos y guiones basadas en el alfabeto.
en 1825 con la creación del electroimán por William Sturgeon.
un electroimán es un tipo de imán en el que el campo magnético se produce mediante el flujo de una corriente eléctrica desapareciendo en cuanto cesa dicha corriente.
Sin embargo fue Samuel Morse quien desarrolló con éxito el electroimán y mejoró el invento de Joseph Henry.
El día del mensaje histórico 24 Mayo 1844, el primer mensaje que se envió fue cuando morse se encontraba en la corte suprema de estados unidos hacia su asistente que se encontraba en Baltimore.
el mensaje enviado correspondía a un párrafo de la biblia que decía
QUÉ NOS HA TRAÍDO DIOS
MATERIALES PARA CREAR UN TELÉGRAFO:
1.- 8 metros de cable de cobre.
2.- un clavo de 7 cm.
3.- pila de 9 volts.
4.- 4 tachuelas.
5.- 3 torsos de madera medida que usted quiera.
6.- 2 metros de alambre recubierto.
7.- 2 tiras de estaño.
VÍDEOS DE LA ELABORACIÓN DEL TELÉGRAFO
lunes, 13 de febrero de 2012
TEORÍA DE LAS TELECOMUNICACIONES
Básicamente tenemos dos tipos de señales: determinísticas y aleatorias. Las
determinísticas tienen un valor conocido en cada instante de tiempo y pueden expresarse
matemáticamente como, por ejemplo, x(t) = 5 cos 10t. Para una señal o forma de onda
aleatoria no es posible dar una expresión explícita como la anterior.
El ejemplo más sobresaliente de este caso, en sistemas de comunicaciones, es el ruido.
Es aleatoria la señal de vídeo, la voz de un locutor de radio, el mensaje de un fax, etc. Lo cual es bastante lógico. Si estas señales fueran determinísticas no tendrían sentido las comunicaciones.
Señales de potencia y de energía
Una señal eléctrica puede ser representada por un voltaje v(t), o una corriente i(t), que
entrega una potencia instantánea p(t) a través de un resistor R.
En sistemas de comunicaciones es común normalizar las ecuaciones anteriores
considerando a R = 1 Ω aunque en realidad pueda tener otro valor. En ese caso las
expresiones anteriores toman la forma general.
Donde x(t) representa una tensión o una corriente, indistintamente. La energía disipada
durante el intervalo de tiempo (- T/2, T/2) por una señal con potencia instantánea expresada
Como veremos más adelante, la performance de un sistema de comunicaciones
depende de la energía de la señal detectada; las señales de mayor energía brindan mayor confiabilidad (menos errores). Por otro lado, la potencia es la velocidad a la que se entrega energía. La potencia determina la tensión eléctrica que debe ser aplicada a un transmisor. En el análisis de sistemas de comunicaciones a menudo es deseable tratar con formas de onda de energía.
Sin embargo, para describir las señales periódicas, que por definición existen para todo tiempo t y tienen energía infinita, es conveniente definir una clase de señales llamadas señales de potencia. Por definición, una señal es de potencia si, y sólo si, tiene potencia mayor que cero y de valor finito para todo.
Densidad espectral
La densidad espectral de una señal caracteriza la distribución de energía o de potencia de una señal en el dominio de la frecuencia. Densidad Espectral de Energía. La energía total de una señal de energía x(t), definida sobre un intervalo (-∞, +∞)
Densidad Espectral de Potencia. La potencia promedio, de una señal real x(t) se define en la ecuación . Si x(t) es una señal periódica con período T0, se la clasifica como una señal de potencia.
representa a los coeficientes complejos de la serie de Fourier (esta es la relación de Parseval para señales periódicas). La función densidad espectral de potencia, Gx(f), de una señal periódica x(t), es una función real, par y no negativa que da la distribución de la potencia de x(t) en función de la frecuencia.
Autocorrelación
Autocorrelación de una señal de energía
La correlación es un proceso de comparación. La autocorrelación se refiere a la
comparación de una señal con una versión desplazada de sí misma. La función de
autocorrelación, Rx(τ), de una señal real de energía x(t).
La función de autocorrelación da una idea de qué tanto se parece una señal a una
versión desplazada (τ unidades en el tiempo) de sí misma. Rx no es una función del tiempo sino que es función de la diferencia de tiempo o desplazamiento τ, entre la función inicial y la función desplazada.
Señales aleatorias
Sea X(A) una variable aleatoria. Representa la relación entre un evento aleatorio A y un número real. Por conveniencia indicaremos a la variable aleatoria solamente por X, quedando implícita su relación con A. La variable aleatoria puede ser discreta o continua. Las variables aleatorias discretas son aquellas que ante un evento, el conjunto de resultados posibles es discreto.
Un proceso aleatorio, X(A, t), puede ser visto como una función de dos variables: un
evento A y el tiempo t. Supongamos N muestras de una función del tiempo Por
conveniencia designaremos a este proceso aleatorio como X(t) y la dependencia con A quedará implícita.
El valor de un proceso aleatorio no puede ser conocido a priori (ya que no se conoce la identidad del evento A). Se busca entonces poder describir este proceso estadísticamente, mediante su función de densidad de probabilidad (fdp). En general, la forma de la fdp de un proceso aleatorio será diferente para diferentes tiempos.
Procesos estacionarios
Un proceso aleatorio X(t) se dice estacionario en sentido estricto si ninguna de sus
propiedades estadísticas son afectadas por un desplazamiento sobre el eje de tiempos. Un proceso aleatorio se dice estacionario en sentido amplio si la media y la autocorrelación no varían con un desplazamiento en el tiempo. Así, un proceso es estacionario en sentido amplio. Estacionario en sentido estricto implica estacionario en sentido amplio, pero no viceversa. La mayoría de los procesos aleatorios usados en sistemas de comunicaciones son estacionarios en sentido amplio.
Ergodicidad.
Para calcular mX y RX(τ) por promediación del ensamble o conjunto,
deberíamos promediar todas las muestras de la función y deberíamos contar con información estadística más amplia que generalmente no está disponible. Cuando un proceso aleatorio pertenece a cierta clase especial llamado proceso ergódico, su promedio temporal es igual al promedio del ensamble y las propiedades estadísticas del proceso pueden determinarse a partir del promedio temporal de una sola muestra. Para que un proceso aleatorio sea ergódico debe ser estacionario en sentido estricto (la inversa no es necesariamente verdadera).
Ruido en sistemas de comunicaciones
El término ruido se refiere a señales eléctricas indeseadas que están siempre presentes
en los sistemas eléctricos. La presencia de ruido superpuesto en una señal tiende a
enmascarar a dicha señal. Esto limita la capacidad del receptor para decidir correctamente
acerca de cuál fue el símbolo transmitido, además de limitar la velocidad de transmisión. Hay
diferentes fuentes de ruido, tanto naturales como artificiales (generados por el hombre).
Hay un tipo de ruido específico llamado ruido térmico o de Johnson que es causado por la agitación térmica natural de los electrones presentes en distintos componentes como ser cables conductores, resistores, transistores, etc. Los mismos electrones que realizan la conducción eléctrica de la señal deseada producen el ruido térmico.
Ruido blanco
La característica distintiva del ruido térmico es que su densidad espectral de potencia es constante para todas las frecuencias que son de interés en la mayoría de los sistemas de comunicaciones. Es decir, una fuente de ruido térmico emana una igual cantidad de potencia por unidad de ancho de banda para todas las frecuencias (desde DC hasta aproximadamente 10 Hz).
Transmisión sin distorsión.
Veamos ahora cuál es el requerimiento de una red ofunción de transferencia para que la transmisión a través de la misma sea sin distorsión. La señal que sale de una línea de transmisión ideal debe ser igual a la señal de entrada, salvo un factor de escala y un retardo. Es decir, una línea de transmisión ideal, sin distorsión, debe relacionar las señales de entrada y de salida
Muchos teoremas importantes de las comunicaciones y de la teoría de la información se basan en la suposición o existencia de canales con un ancho de banda limitado
(estrictamente). Sin embargo, considerar un ancho de banda así implica considerar una señal de duración infinita, lo cual es impracticable. Por otra parte, considerar que el ancho de banda se extiende de forma infinita también es irrazonable. Realmente, no hay una definición universal para el ancho de banda.
martes, 7 de febrero de 2012
Análisis de Fourier
Las ondas armónicas continuas que hemos estudiado no existen realmente, ya que todos los movimientos ondulatorios están limitados tanto espacial como temporalmente. Utilizando el análisis de Fourier y la transformada de Fourier se pueden describir formas de ondas más complejas como las que producen los instrumentos musicales.
A primera vista, parece que el problema de analizar formas de ondas complejas representa una tarea formidable. Sin embargo, si la forma de la onda es periódica, se puede representar con una precisión arbitraria, mediante la superposición de un número suficientemente grande de ondas senoidales que forman una serie armónica.
Una vez elegido la función, introducimos los parámetros requeridos en los controles de edición y pulsamos el botón cuyo título da nombre a la función.
La separación entre estos segmentos verticales es inversamente proporcional al periodo de la función, por tanto, para una función aperiódica (periodo infinito), la envolvente de los extremos de los segmentos verticales define una curva continua denominada transformada de Fourier.
Pulsando en el botón titulado Anterior<< podemos volver a la aproximación anterior y compararla con la siguiente.
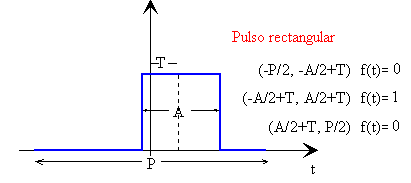
El pulso rectangular nos permite verificar que son nulos los coeficientes bi en una función cuya simetría es par. Probar el siguiente ejemplo:
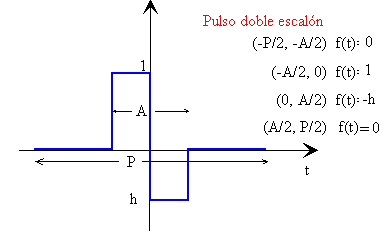
El pulso doble escalón nos permite verificar que son nulos los coeficientes ai en una función cuya simetría es impar. Probar el siguiente ejemplo:
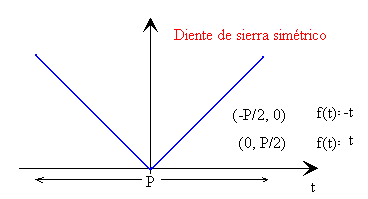
Ejemplo:
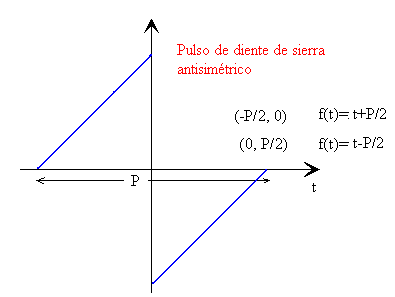
- Rectangular
- Doble escalón
- Diente de sierra 1
- Diente de sierra 2
- En la parte superior, la función f(t) elegida y las sucesivas aproximaciones de dicha función.
- En la parte central, el armónico actual, en color azul ai·cos(ix) y en color rojo bi sin(ix).
- En la parte inferior, mediante segmentos verticales, la magnitud relativa de los coeficientes de Fourier, a la izquierda en color azul los coeficientes ai, y a la derecha en color rojo los coeficientes bi.
La separación entre estos segmentos verticales es inversamente proporcional al periodo de la función, por tanto, para una función aperiódica (periodo infinito), la envolvente de los extremos de los segmentos verticales define una curva continua denominada transformada de Fourier.
Pulsando en el botón titulado Anterior<< podemos volver a la aproximación anterior y compararla con la siguiente.
Ejemplos
Pulso rectangular

El pulso rectangular nos permite verificar que son nulos los coeficientes bi en una función cuya simetría es par. Probar el siguiente ejemplo:
- Periodo, 5.0
- Anchura, 2.0
- Traslación, 0.0.
- Periodo, 5.0
- Anchura, 2.0
- Traslación, 0.5.
Pulso doble escalón

El pulso doble escalón nos permite verificar que son nulos los coeficientes ai en una función cuya simetría es impar. Probar el siguiente ejemplo:
- Periodo, 3.0
- Anchura, 2.0
- Profundidad, 1.0.
- Periodo, 3.0
- Anchura, 2.0
- Profundidad, 0.5.
Pulso diente de sierra simétrico

Ejemplo:
- Periodo, 4.0.
Pulso diente de sierra antisimétrico

Suscribirse a:
Comentarios (Atom)




.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
